A collection of time series analysis exercises
그동안 익힌 시계열 분석관련 내용을 정리/요약해둔 곳입니다.
시계열(Time-Series) 자료: 어떠한 대상을 여러 시점에서 관찰한 일련의 기록, 종단 자료
-
자기상관성을 가진다. 시계열, 종단면 데이터에서 어떠한 관측치는 독립적이지 않고 같은 확률분포를 가졌다고도 볼 수 없다.
-
시간, 시점들 사이 관계를 통해 미래를 예측하는 Forecasting이 주된 목적이다.
시계열의 주요 번동 4 가지
랜덤(무작위), 계절, 추세, 계절추세(복합) 변동
시계열 다루기-
차분: 직전의 값과의 차이를 구하여 장기적인 추세를 제거하고 "정상화"시킬 때 쓴다. 계절성을 제거할 때는 1년 단위로 차분하는 계절 차분이라고도 한다. (and 역차분, 윈도잉, 합/교집합 등 코드 참조)
-
평활화(smoothing): 과거의 값을 다룰 때 주로 쓰는 기법. 주로 계절적이고 불규칙한 변동들을 제거한다. (by aggregating) 대표적인 방법으로 MA(이동평균기법), 지수평활법 등이 있다.
*여기서 과거의 관측치를 통해 현재의 상태를 추정할 떄 "필터링(Filtering)"이라고도 하고, 미래의 상태를 추정할 떄 "예측(Forecasting)"이라고 하기도 한다.
- 요소분해(decomposing): 어떠한 시계열을 랜덤, 계절, 추세 변동으로 분해한다. 이 때 중요한 것은 랜덤변동이 어떠한 다른 변동이 없는 "정상시계열"을 만족해야 한다는 것이다.
조건: Stationary process
횡단면 데이터(한 시점의 cross sectional한 관측치)와 달리 시계열 데이터는 자기상관에서 자유로울 수 없다. 즉, 어떠한 관측치는 독립적이지 않으며 이전의 관측치에 영향을 받고 있다. (i.i.d 가정 불가능)
이에 bias를 줄이고 객관적인 예측을 하기 위해서 시계열로 구성된 데이터가 가지는 내재적인 패턴을 제거해야 한다.
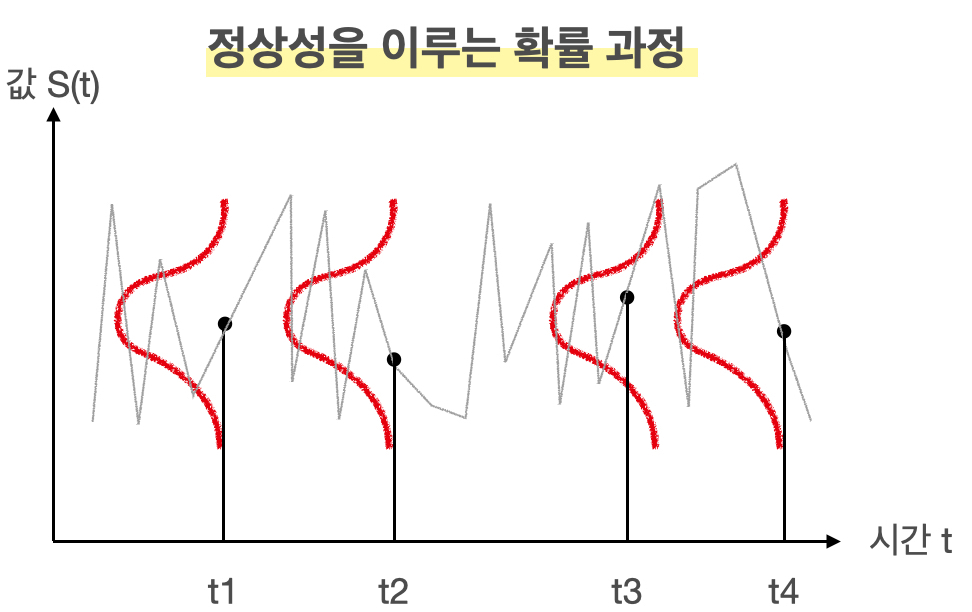
정상시계열: 어떠한 데이터가 가지고 있는 특징들(추세, 계절, 순환 등)을 제거하여 랜덤화된 시계열을 말하는데, 시점에 따라 평균과 분산이 동일하여 같은 확률분포로써 예측이 가능하다.
*강정상성: 어떤 시점들간의 결합분포가 모두 동일하다.
*약정상성: 1. 어떤 시점에서든 기댓값이 같고 2. 분산이 무한대로 팽창하지 않으며 3. 시점간 공분산이 "시차"에만 의존한다. (약정상성만 충족시켜도 정상성을 가진다고 판단하는게 일반적이다.)
시계열 데이터의 필수 모델링 과정: 정상성 체크 -> 정상성 처리(비정상 시계열인 경우) -> 정상성 검증(Test), 보통 ADF test를 진행한다. (H0: 비정상시계열이다.)
>> Case 1) 정상 시계열
- AR model
자기자신의 과거 값으로 선형 결합하여 변동을 설명하고 관심 있는 변수를 예측한다.
AR(p): p차 자기회귀 모형
y_t = c + Φ1 * y_t-1 + Φ2 * y_t-2 + ... + Φp * y_t-p + ε_t *ε_t는 잔차이자 백색소음
- MA model
평활화(smoothing) 기법을 적용한 모델로, 정상시계열인 백색소음을 평활화하여 남아있는 변동을 설명한다.
MA(q) : q차 이동평균 모형
y_t = c + Θ1 * ε_t-1 + Θ2 * ε_t-2 + ... + Θq * ε_t-q + ε_t
- ARMA model
AR + MA
p개의 자기 자신의 과거값과 q개의 과거 백색 잡음의 선형 결합
>> Case 2) 비정상 시계열
- ARIMA model
ARMA모델에 차분의 개념이 포함된 모델. 즉, 비정상시계열을 먼저 정상시계열로 바꾼 뒤(by diffrencing) AR과 MA 모델을 결합한다.
ARIMA(p, d, q) : d차 차분한 데이터에 AR(p) 모형과 MA(q) 모형을 합친 모형
>> ACF , PACF
ACF에서 q결정(MA모델의 자기상관이 최소화되는 지점), PACF에서 p결정(AR모델의 자기상관이 최소화되는 지점)
1. VAR(벡터자기회귀, Vector AutoRegressive Model)
현실세계의 현상은 대부분 하나의 요인이 아닌 여러 요인에 의해 일어난다.
즉, 시간에 따라 변화하는 여러 현상들 또한 그 시계열 간의 상관관계가 존재한다.(독립적일 수가 없다.)
이에 벡터자기회귀(VAR)는 k개의 AR식, 여러 시계열을 벡터로 쌓아 현상을 예측한다.
단일 시계열 AR과 다른 점은 설명변수로 자기 자신의 lag뿐 아니라 다른 변수들의 lag도 포함한다는 것이다.
2. 변동성 모형 (ARCH, GARCH)
대부분의 시계열 현상, 특히 사회과학에서 나타나는 현상은 등분산성을 충족하지 못한다.
즉, 시간이 흐를수록 그 변동 폭 또한 변화하는 것인데, 보통은 그 폭이 증가하는 추세를 보인다.
이러한 상황에서 특히 금융도메인에서는 변화하는 y값 이외에도 그 변동성까지 통제하고 관리해야 할 필요성을 가지기 마련이다.
+
- 조건부 분산
x 의 값을 알고 있을 때 이에 대한 조건부확률분포 p(y|x)의 분산
예측문제의 관점으로 보면 조건부분산은 예측의 불확실성를 의미하기도 한다.
GARCH 모델은 ARCH 모델을 Generalized한 모델이다.
ARCH는 그 계수인 q에 따라 모형이 매우 복잡해지고 성능 또한 오르지 않는 문제가 빈번히 발생한다.(어느정도 시점까지의 변동을 이용하여 예측할 것인가)
GARCH모델은 ARCH를 일반화하여 추정해야할 모수를 줄이고, 분산이 자체 시차값(lagged values)에 의존하도록 하여 더욱 효과/효율적인 분석을 가능하게 한다.
time-series or ordered task에서 딥러닝이 가지는 장점
-
상대적으로 긴 t시점에 적합하다. (arima는 정상성 등의 제약 때문에 긴 변동을 설명하기에는 무리가 있다.)
-
다변량 X, 다변량 Y 문제에 적용이 가능하다.
-
순환, "기억(Memory)"의 개념이 적용된다. (즉, 자기상관을 그대로 받아 모델링한다.)
-
수치, 숫자 뿐만 아니라 영상, 문자, 행동기록(로그) 등 비정형 데이터를 다룰 수 있다.
- Vanilla RNN
바닐라, 즉, 기본 RNN 모델은 딥러닝에 Recurrent한 구조를 접목한 모델로 sequential한 데이터를 다루는 데 이용된다.
그러나, 이는 학습이 점차 장기적으로 이어질 떄 기울기 소멸 혹은 폭주의 문제로 temporal한 dependency를 파악하는 데 한계가 있다.
- LSTM
LSTM은 RNN 구조에 내부의 cell state와 4개의 gate를 두어 정보를 효과적으로 처리한다.
LSTM은 vanilla RNN의 장기 의존성 문제를 해결하였다.
Blog Review -> RNN, LSTM
코드는 위 폴더를 참고해주세요!