-
Notifications
You must be signed in to change notification settings - Fork 70
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
More complex maze generation by circular implementation of the grid #32
Comments
|
That sounds & looks pretty awesome! Just to make sure I'm on the same page about the example above, The maze has 5 rows and 4 columns? I think it could be feasible with the current code base, but a more accurate answer would require knowing if this can be solved using the current solution methods. It sounds like we would want to handle this and square mazes differently. This would mean creating a super class, called One other issue may be (depending on how you do it) linking the columns together. I'm sure there are algorithms that depend on proper column endings. Having a finer mesh would be awesome, maybe you could set that as a default argument and let the user override it! As for matplotlib, @jostbr did all of the visualization stuff and probably has some good input. |
|
I agree, this sounds very cool! @ThomasThelen In the example I think it is 5 rows and 2^(5+2) = 128 columns by @kkaushikvarma logic (although I don't understand the "+2" in the exponent). I too am not 100% sure to what extent we can use the code already in place directly for the circular mazes and that the main difference would by in the visualization. As you guys mentioned there might be challenges with the periodic behaviour of the columns, but if it turns out the generation and solution can be handled basically by the algorithms that's already in place, then it definitely should be doable. However the visualization would by quite different, but I believe matplotlib has possibilities to create create the sort of curves we would need, but it would be more complex than the rectangular maze. |
|
@ThomasThelen @jostbr Thank you for responding to my suggestion. So, if you have 4 rows in the maze, there would be (4+8+16+32) number of columns So far, I have successfully managed to implement the generation of the circular maze without any phenomenal changes to your base algorithm (honestly, your code was pretty consistent and could easily be applied) The following are the main changes I've made: Neighbours: The rest of the changes were minor additions to different functions. As for the visualization, I've done some digging and I'm generating each cell by drawing two arcs for the outer and inner walls and connecting them The visualization works but there seems to be a glitch that I'm still trying to figure out. The problem is that there seems a synchronization issue with the expected figure and angle inputs. This is causing additional walls between cells that ought not to have walls between them. But nevertheless, we know that the visualization works and just requires some operational changes. Below are the outputs of the visualizer: Now, none of the visualizations are perfect mazes as a result of the synchronization problem but I've manually taken the outputs of Anyway, ignore that issue for the time because, as you might have noticed, there's another problem which requires a higher priority. The layers are becoming extremely small with an increase in rows. This is the main downside to increasing the number of columns every row. An alternative to this would be to leave the number of columns consistent but the issue then would be that the cells in the inner layers would be too small and the cells on the outer layers would be too wide. I'd like to know if you guys have any solutions for this. A solution I'd propose is to bring down the rate of increase of columns by 2 and also increase the gap between any two circles. I'll structure the code without interfering with the functioning of your maze program before committing changes. I'll be adding an exception to generate a |
|
I've moved to the new relation: columns = 2^(int(row/2)+2) and the maze is being generated beautifully. I've also corrected the visualization problem. Verify the pull request so we can move further. |
|
Great effort! I merged the pull request now. I agree, the choice of columns = 2^(int(row/2)+2) seems to work great. Impressive work on both the cells and generation as well as the visualization. Looks great! |
|
See my comments on the commit; with the way things are currently done, adding new features is going to be difficult. Can we un do the merge? We should either create a new branch under |
|
Okay, yeah, I see what you mean. Might need a little restructure nefore it should be merged with |




It would be great if a circular maze, which is usually more complex to be comprehended by the human mind, could be implemented using the algorithm that is already here.
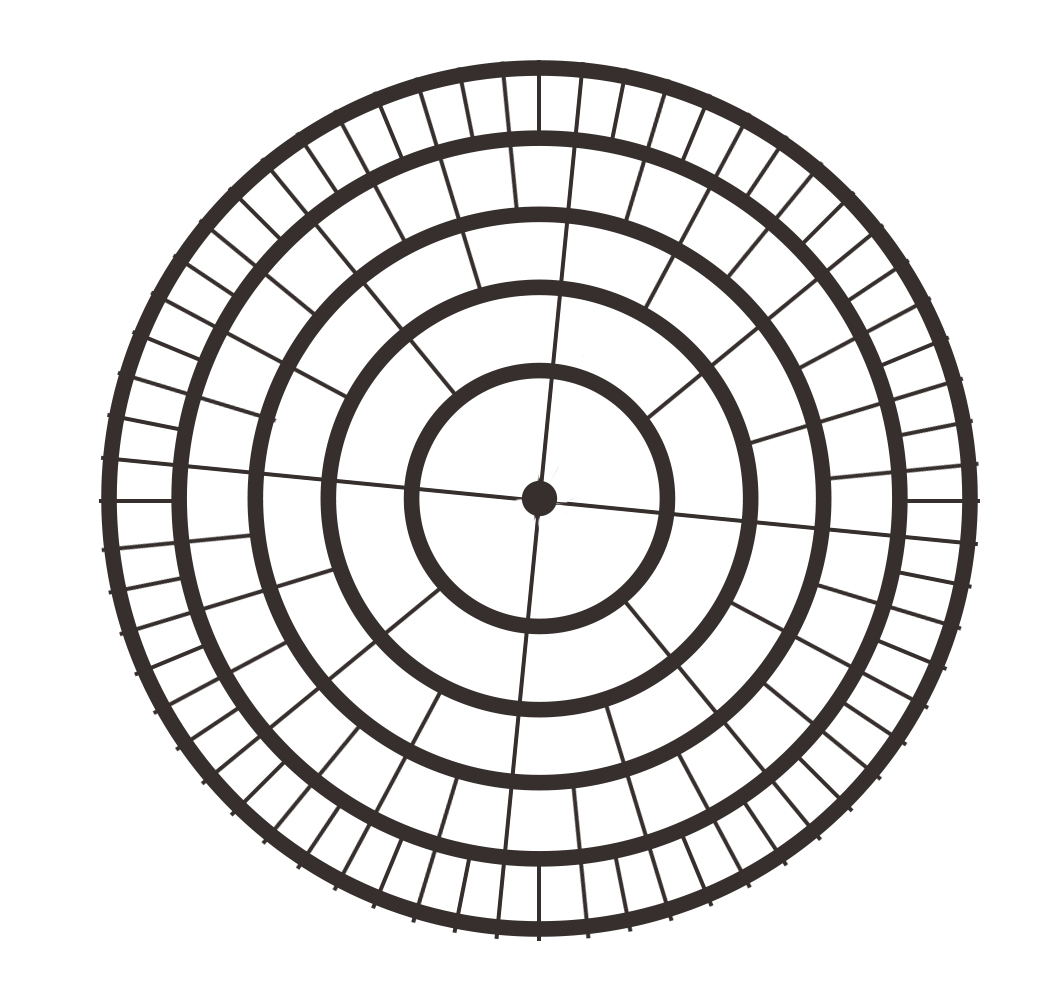
What I have in mind is the following cell structure:
The design above is not geometrically optimal but could be implemented the following way:
-That would imply, only the rows (number of circles) will be given as input and the number of columns would be : pow(2,rows+2)
-The condition for a cell to be start/exit would be row = num_rows-1
I have implemented the above condition but I am yet to commit the changes as visualizing this in matplotlib is not as simple as doing that for a grid. The following is a manual visualization from the raw outputs of
generate_maze.Please do let me know if you're more interested in this and have ideas about visualzing this implementation in matplotlib
The text was updated successfully, but these errors were encountered: