040 Multithreading.jl

import Pkg; Pkg.activate(@__DIR__); Pkg.instantiate()

# # Multithreading
#
# Now we're finally ready to start talking about running things on multiple
# processors! Most computers (even cell phones) these days have multiple cores
# or processors — so the obvious place to start working with parallelism is
# making use of those from within our Julia process.
#
# The first challenge, though, is knowing precisely how many "processors" you have.
# "Processors" is in scare quotes because, well, it's complicated.

versioninfo(verbose = true)

#-

using Hwloc
Hwloc.num_physical_cores()

# What your computer reports as the number of processors might not be the same
# as the total number of "cores". While sometimes virtual processors can add
# performance, parallelizing a typical numerical computation over these virtual
# processors will lead to significantly worse performance because they still
# have to share much of the nuts and bolts of the computation hardware.

#-

# Julia is somewhat multithreaded by default! BLAS calls (like matrix multiplication) are
# already threaded:

using BenchmarkTools
A = rand(1000, 1000);
B = rand(1000, 1000);
@benchmark $A*$B

# This is — by default — already using all your CPU cores! You can see the effect
# by changing the number of threads (which BLAS supports doing dynamically):

using LinearAlgebra
BLAS.set_num_threads(1)
@benchmark $A*$B
BLAS.set_num_threads(4)
@benchmark $A*$B

# ## What does it look like to implement your _own_ threaded algorithm?

using .Threads

nthreads()

# Julia currently needs to start up knowing that it has threading support enabled.
#
# You do that with a environment variable. To get four threads, start Julia with:
#
# ```
# JULIA_NUM_THREADS=4 julia
# ```

run(`env JULIA_NUM_THREADS=4 julia -E 'using .Threads; nthreads()'`)

# The other way to do it is in JuliaPro itself:
#
# * Go to the Julia Menu -> Settings -> Number of Threads
# * By default it'll choose a "good" number for you

threadid()

# So we're currently on thread 1. Of course a loop like this will
# just set the first element to one a number of times:

A = zeros(Int, nthreads())
for i in 1:nthreads()
    A[i] = threadid()
end
A

# But if we prefix it with `@threads` then the loop body is divided between threads!

@threads for i in 1:nthreads()
    A[i] = threadid()
end
A

# So let's try implementing our first simple threaded algorithm — `sum`:

function threaded_sum1(A)
    r = zero(eltype(A))
    @threads for i in eachindex(A)
        @inbounds r += A[i]
    end
    return r
end

A = rand(10_000_000)
threaded_sum1(A)
@time threaded_sum1(A)

#-

sum(A)
@time sum(A)

# Whoa! What happened? Not only did we get the wrong answer, it was _slow_ to get it!

function threaded_sum2(A)
    r = Atomic{eltype(A)}(zero(eltype(A)))
    @threads for i in eachindex(A)
        @inbounds atomic_add!(r, A[i])
    end
    return r[]
end

threaded_sum2(A)
@time threaded_sum2(A)

# Alright! Now we got the correct answer (modulo some floating point associativity),
# but it's still slower than just doing the simple thing on 1 core.

threaded_sum2(A) ≈ sum(A)

# But it's still slow! Using atomics is much slower than just adding integers
# because we constantly have to go and check _which_ processor has the latest
# work! Also remember that each thread is running on its own processor — and
# that processor also supports SIMD!  Well, that is if it didn't need to worry
# about syncing up with the other processors...

function threaded_sum3(A)
    r = Atomic{eltype(A)}(zero(eltype(A)))
    len, rem = divrem(length(A), nthreads())
    @threads for t in 1:nthreads()
        rₜ = zero(eltype(A))
        @simd for i in (1:len) .+ (t-1)*len
            @inbounds rₜ += A[i]
        end
        atomic_add!(r, rₜ)
    end
    # catch up any stragglers
    result = r[]
    @simd for i in length(A)-rem+1:length(A)
        @inbounds result += A[i]
    end
    return result
end

threaded_sum3(A)
@time threaded_sum3(A)

# Dang, that's complicated. There's also a problem:

threaded_sum3(rand(10) .+ rand(10)im) # try an array of complex numbers!

# Isn't there an easier way?

R = zeros(eltype(A), nthreads())

#-

function threaded_sum4(A)
    R = zeros(eltype(A), nthreads())
    @threads for i in eachindex(A)
        @inbounds R[threadid()] += A[i]
    end
    r = zero(eltype(A))
    # sum the partial results from each thread
    for i in eachindex(R)
        @inbounds r += R[i]
    end
    return r
end

threaded_sum4(A)
@time threaded_sum4(A)

# This sacrifices our ability to `@simd` so it's a little slower, but at least we don't need to worry
# about all those indices! And we also don't need to worry about atomics and
# can again support arrays of any elements:

threaded_sum4(rand(10) .+ rand(10)im)

# ## Key takeaways from `threaded_sum`:
#
# * Beware shared state across threads — it may lead to wrong answers!
#     * Protect yourself by using atomics (or [locks/mutexes](https://docs.julialang.org/en/v1/base/multi-threading/#Synchronization-Primitives-1))
#     * Better yet: divide up the work manually such that the inner loops don't
#       share state. `@threads for i in 1:nthreads()` is a handy idiom.
#     * Alternatively, just use an array and only access a single thread's elements

#-

# # Beware of global state (even if it's not obvious!)
#
# Another class of algorithm that you may want to parallelize is a monte-carlo
# problem. Since each iteration is a new random draw, and since you're interested
# in looking at the aggregate result, this seems like it should lend itself to
# parallelism quite nicely!

using BenchmarkTools

#-

function serialpi(n)
    inside = 0
    for i in 1:n
        x, y = rand(), rand()
        inside += (x^2 + y^2 <= 1)
    end
    return 4 * inside / n
end
serialpi(1)
@time serialpi(100_000_000)


# Let's use the techniques we learned above to make a fast threaded implementation:

function threadedpi(n)
    inside = zeros(Int, nthreads())
    @threads for i in 1:n
        x, y = rand(), rand()
        @inbounds inside[threadid()] += (x^2 + y^2 <= 1)
    end
    return 4 * sum(inside) / n
end
threadedpi(240)
@time threadedpi(100_000_000)

# Ok, now why didn't that work?  It's slow! Let's look at the sequence of random
# numbers that we generate:

import Random
Random.seed!(0)
N = 20000
Rserial = zeros(N)
for i in 1:N
    Rserial[i] = rand()
end
Rserial

#-

Random.seed!(0)
Rthreaded = zeros(N)
@threads for i in 1:N
    Rthreaded[i] = rand()
end
Rthreaded

#-

Set(Rserial) == Set(Rthreaded)

# Aha, `rand()` isn't (currently) threadsafe! It's mutating (and reading) some global each
# time to figure out what to get next. This leads to slowdowns — and worse — it
# skews the generated distribution of random numbers since some are repeated!!
#
# Note: on the upcoming Julia 1.3 it is now threadsafe by default! Here's how
# we can emulate it on prior versions:

const ThreadRNG = Vector{Random.MersenneTwister}(undef, nthreads())
@threads for i in 1:nthreads()
    ThreadRNG[Threads.threadid()] = Random.MersenneTwister()
end
function threadedpi2(n)
    inside = zeros(Int, nthreads())
    len, rem = divrem(n, nthreads())
    rem == 0 || error("use a multiple of $(nthreads()), please!")
    @threads for i in 1:nthreads()
        rng = ThreadRNG[threadid()]
        v = 0
        for j in 1:len
            x, y = rand(rng), rand(rng)
            v += (x^2 + y^2 <= 1)
        end
        inside[threadid()] = v
    end
    return 4 * sum(inside) / n
end
threadedpi2(240)
@time threadedpi2(100_000_000)

# As an aside, be careful about initializing many `MersenneTwister`s with
# different states. Better to use [`randjump`](https://docs.julialang.org/en/v1/manual/parallel-computing/#Side-effects-and-mutable-function-arguments-1) to skip ahead for a single state.

#-

# # Beware oversubscription
#
# Remember how BLAS is threaded by default? What happens if we try to `@threads`
# something that uses BLAS?

Ms = [rand(1000, 1000) for _ in 1:100]
function serial_matmul(As)
    first_idxs = zeros(length(As))
    for i in eachindex(As)
        @inbounds first_idxs[i] = (As[i]'*As[i])[1]
    end
    first_idxs
end
serial_matmul(Ms[1:1]);
@time serial_matmul(Ms);

#-

using LinearAlgebra
BLAS.set_num_threads(nthreads()) # Explicitly tell BLAS to use the same number of threads
function threaded_matmul(As)
    first_idxs = zeros(length(As))
    @threads for i in eachindex(As)
        @inbounds first_idxs[i] = (As[i]'*As[i])[1]
    end
    first_idxs
end
threaded_matmul(Ms[1:1])
@time threaded_matmul(Ms);

#-

BLAS.set_num_threads(1)
@time threaded_matmul(Ms);

#-

@time serial_matmul(Ms) # Again, now that BLAS has just 1 thread

# # Beware "false sharing"

#-

# Remember the memory latency table?
#
#
# | System Event                   | Actual Latency | Scaled Latency |                          |
# | ------------------------------ | -------------- | -------------- | ------------------------ |
# | One CPU cycle                  |     0.4 ns     |     1 s        | ← work happens here     |
# | Level 1 cache access           |     0.9 ns     |     2 s        |                          |
# | Level 2 cache access           |     2.8 ns     |     7 s        |                          |
# | Level 3 cache access           |      28 ns     |     1 min      |                          |
# | Main memory access (DDR DIMM)  |    ~100 ns     |     4 min      | ← we have control here  |
#
# This is what a typical modern cpu looks like:
#
# ![Intel Core i7](https://raw.githubusercontent.com/JuliaComputing/JuliaAcademyData.jl/master/courses/Parallel_Computing/images/i7.jpg)
#
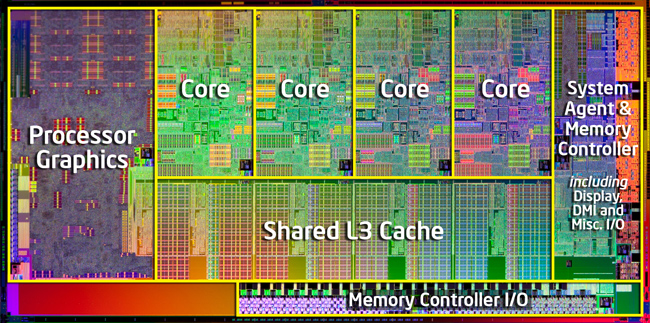
# Multiple cores on the same processor share the L3 cache, but do not share L1 and L2 caches! So what happens if we're accessing and mutating data from the same array across multiple cores?
#
# ![Cache coherency](https://raw.githubusercontent.com/JuliaComputing/JuliaAcademyData.jl/master/courses/Parallel_Computing/images/false-sharing.gif)
#
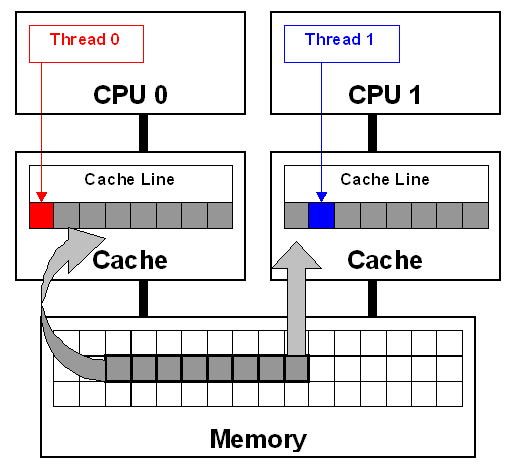
# Unlike "true" sharing — which we saw above — false sharing will still return the correct answer! But it does so at the cost of performance. The cores recognize they don't have exclusive access to the cache line and so upon modification they alert all other cores to invalidate and re-fetch the data.

function test(spacing)
    a = zeros(Threads.nthreads()*spacing)
    b = rand(1000000)
    calls = zeros(Threads.nthreads()*spacing)
    @threads for i in eachindex(b)
        a[Threads.threadid()*spacing] += b[i]
        calls[Threads.threadid()*spacing] += 1
    end
    a, calls
end
@benchmark test(1);
@benchmark test(8);

#-

# ## Further improvements coming here!
#
# PARTR — the threading improvement I discussed at the beginning aims to address
# this problem of having library functions implemented with `@threads` and then
# having callers call them with `@threads`. Uses a state-of-the-art work queue
# mechanism to make sure that all threads stay busy.

#-

# # Threading takeaways:
#
# * It's easy! Just start Julia with `JULIA_NUM_THREADS` and tack a `@threads` on your loop
# * Well, not so fast
#     * Be aware of your hardware to set `JULIA_NUM_THREADS` appropiately
#     * Beware shared state (for both performance and correctness)
#     * Beware global state (but the built-in global state is improving!)
#     * Beware false sharing (especially with multiple processor chips)
# * We need to think carefully about how to design parallel algorithms!