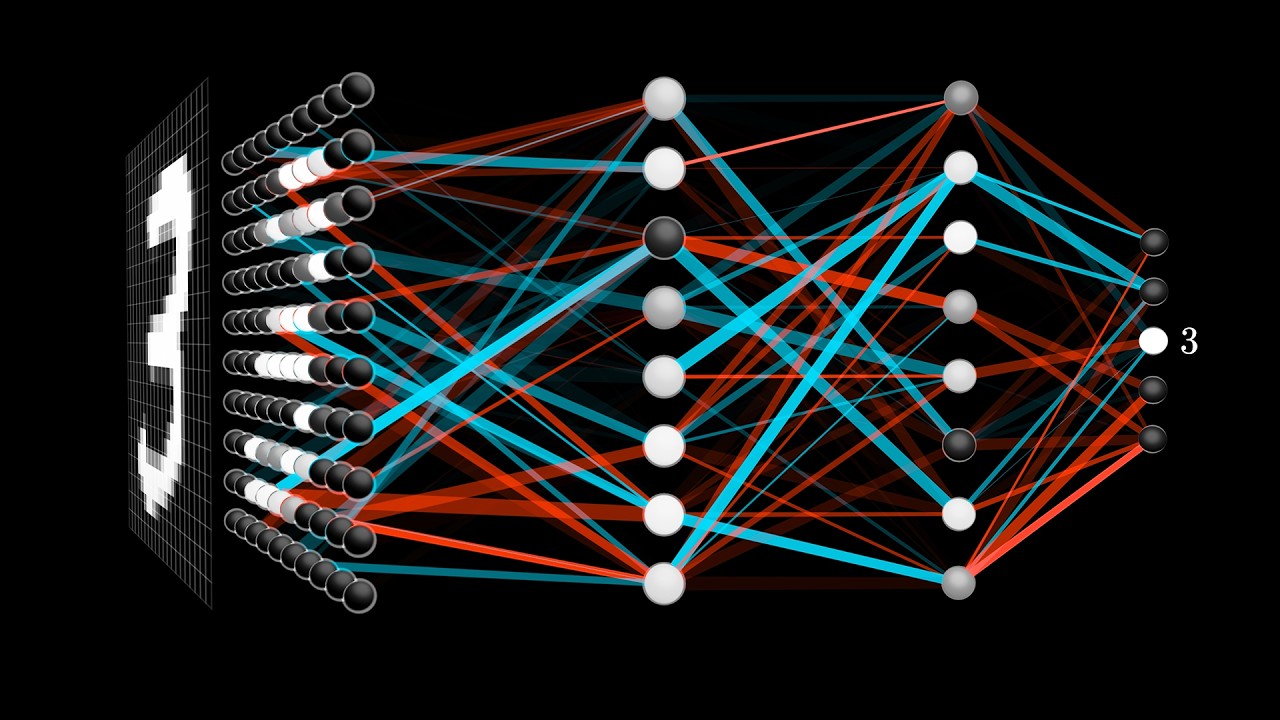
In the Winter of 2019 I started an interest in neural networks. I took a look at TensorFlow but didn't really understand what I was doing, so I decided to write my own little framework to understand the underling math and implementation.
For the basic understanding of the underling idea, I took a look at the great series that Grandsenderson (3blue1broun) published on YouTube.
To actually see how someone could implement such a system like this, I skipped through some coding train episodes in this playlist:
I first thought about how I would interface to the network that I wanted X amount of input, hidden and output layers with X_n amount of layer neurons. I went thought a couple of iterations an ended up at a simple array filled with integers like this:
network_size = [2, 4, 8, 4, 2]So this array should create a network with 2 input neurons, 3 hidden layers with 4, 8, 4 neurons respectively and 2 output neurons.
To initialize the weights and biases, I came up with this
# i loop though every element in the network's size
# and enumerate it
for index, layer_size in enumerate(self.__size):
# we check if we are at the n-1th layer of the network
# as we later check the size of the next layer to generate
# the corresponding amount of weights and biases
if index != len(self.__size)-1:
# here we grab the number of neurons
# of the above-mentioned next layer
connecting_layer_size = self.__size[index+1]
# this is pretty straight forward,
# we just create one random bias for every neuron
# in the next layer
self.biases.append(
[
random.random() for _ in range(connecting_layer_size)
]
)
# this next list comprehension is a bit more complicated
# we want to create a connection between every neuron in
# the current layer to every single neuron in the next layer
# that is why we first range through every neuron on the current layer
# for every neuron on the next, creating randomly initialized weights on the way
self.weights.append([
[
random.random() for _ in range(layer_size)
]
for _ in range(connecting_layer_size)
])At the end of this loop, we should have all our weight and biases initialized. We initialized them randomly to speed up the training process in the beginning.
Cool, now we have a bunch of weights and biases that somehow represents the structure of our network, but we actually have to still write the part that performs the matrix multiplications propagation the input thought the layers.
This is our forward loop:
# this function's input parameter is an array of floats, for our network from before this could be something like this [1.2040632234, -0.3424677687]
def Feedforward(self, inputs):
# we assign outputs here to the inputs because the network generates an output for every layer which is passed on to the next as it's input, so this is just a decision on how to name what
outputs = inputs
# now we are looping through weights and biases that we have initialized in the step before
# in the first case, layer_weights would be a 2 dimensional array of size 4 x 2 because we have 2 connections for every neuron in the next layer (the next layer has 4 neurons)
for layer_weights, layer_bias in zip(self.weights, self.biases):
# here we reassign the result of the first layer to the outputs to use in the next layer
outputs = [
# now we start calculation the result at the output of the neuron in the next layer by looping though its weights and grabbing the bias to add to the result
# we use the sigmoid function to map the output to a range between -1 and 1 to prevent the output at each layer to grow bigger and bigger and bigger
self.__Sigmoid(
# we add the result of multiplied every weight of the neuron by the inputs, so in the first layer we would multiply 1.2040632234 * layer_weights[0] and then -0.3424677687 * layer_weights[0]. After the summation over the two number, we add the bias.
sum([
neuron_weight*inpt for neuron_weight, inpt in zip(
neuron_weights, outputs
)
]) + bias)
for neuron_weights, bias in zip(layer_weights, layer_bias)
]
# And that's it, after 4 iterations of this loop we should have our outputs at the last layers, and we just have to return them.
return outputs Now that works and all, but if we actually give the network some data, for example [1, 0], and we want it to flip the two input the network probably performs terribly. So to train the network how to do that task, we have to manipulate its parameters. In this case, we have to find the right weights and biases for the 4 layers after the input. We could just do our first step of generating a new random weight over and over again until we get the right result for the input, but that would take a really long time and would be really inefficient. It would be better i we knew how our weight and biases are actually wrong with respect to our current input and output. Luckily, this is possible
#Documentation is in progress - sorry
def __Backpropagate(self, inputs=[], targets=[]):
outputs = inputs
activations = [inputs]
for layer_weights, layer_bias in zip(self.weights, self.biases):
outputs = [
self.__Sigmoid(
sum(
[
neuron_weight*inpt for neuron_weight, inpt in zip(neuron_weights, outputs)
]
) + bias)
for neuron_weights, bias in zip(layer_weights, layer_bias)
]
activations.append(outputs)
error = self.__Calculate_error(targets, outputs)
errors = [error]
for layer in self.weights[::-1]:
error = [
sum(pre_neuron_erros)for pre_neuron_erros in zip(
*[
[
(n/sum(pre_neurons))*neuron_error for n in pre_neurons
]
for neuron_error, pre_neurons in zip(error, layer)
])
]
errors.append(error)
delta_biases = []
delta_weights = []
for layer_activation, pre_layer_activation, layer_errors in zip(
activations[::-1],
activations[-2::-1],
errors
):
delta_layer_biases = []
delta_layer_weights = []
for neuron_activation, neuron_errors in zip(layer_activation, layer_errors):
e = self.__Derivative(neuron_activation) * neuron_errors
delta_neuron_biases = e
delta_neuron_weights = [
e*pre_neuron_activation for pre_neuron_activation in pre_layer_activation
]
delta_layer_biases.append(delta_neuron_biases)
delta_layer_weights.append(delta_neuron_weights)
delta_biases.append(delta_layer_biases)
delta_weights.append(delta_layer_weights)
delta_biases = delta_biases[::-1]
delta_weights = delta_weights[::-1]
return delta_weights, delta_biases