This filter is my best filter I have ever used before. I have been a long time fan of Kalman Filters and I started with the linear Kalman Filter(KF). It works good, but the problem with KF is that it's only for linear systems. The KF filter has its origins from 1960.
The next generation of KF was the Extended Kalman Filter(EKF) and it was a successful filter because it takes account to non-linearity. The only drawback with EKF is that it’s too difficult to do in real time practice at a microcontroller. The EKF has its orgins from 1985. Notice that EKF is just a linearized KF by using jacobians, which is not very easy to use in practice.
So therefore, another filter was created to replace EKF, it was Unscented Kalman Filter(UKF) and it was the most successful kalman filter ever made. It has its orgins from 1997, when the first paper was released. “A New Extension of the Kalman Filter to Nonlinear Systems” by Simon J. Julier and Jeffrey K. Uhlmann.
I have created created UKF in both C code and MATLAB code. Notice that there is a Square Root Uncented Kalman Filter too. It's much better than regular Uncented Kalman Filter because it's more stable.
/*
============================================================================
Name : ukf.c
Author : Daniel Mårtensson
Version : 1.0
Copyright : MIT
Description : Filter with Unscented Kalman Filter
============================================================================
*/
#include "CControl/Headers/Functions.h"
int main() {
// Initial parameters
uint8_t L = 1; // How many states we have
float a = 0.5; // Alpha value
float b = 2; // Beta value
float k = 1; // Kappa value
float Q[1 * 1] = { 0.0001 }; // Initial disturbance covariance matrix
float R[1 * 1] = { 2 }; // Initial noise covariance matrix
float P[1 * 1] = { 1 }; // Initial covariance matrix
float xhat[1] = { 15 }; // Initial estimated state, a rule of thumb: Use a regular measurement only
float zk[1] = { 0 }; // This is our measurement
float u[1] = { 0 }; // u is not used in this example due to the transition function not using a input signal
// Our transition function is a random variable
void ukf_transition(float x[], float s[], float u[], uint8_t L) {
uint8_t N = 2 * L + 1;
float a[L];
float r[1];
for (uint8_t j = 0; j < N; j++) {
for (uint8_t i = 0; i < L; i++)
a[i] = s[i * N + j]; // Extract one column from matrix s
randn(r, 1, 0, 1); // Create one random value with mean 0 and deviation 1
x[j] = std(a, L) * r[0] + mean(a, L);
}
}
// Data of a laser measurement with mean 14 and deviation 1
float X[500]; // Estimated
float data[500] = { 15, 14, 13, 14, 15, 14, 16, 14, 15, 14, 13, 15, 14, 15,
13, 14, 16, 14, 15, 14, 15, 14, 15, 14, 15, 14, 15, 16, 15, 14, 13,
14, 15, 13, 14, 13, 14, 15, 14, 15, 13, 15, 14, 16, 14, 13, 14, 15,
13, 15, 14, 15, 13, 14, 15, 13, 15, 14, 13, 14, 15, 16, 13, 15, 14,
13, 15, 14, 16, 14, 16, 15, 17, 14, 16, 14, 13, 16, 13, 15, 16, 15,
14, 15, 14, 12, 15, 13, 14, 13, 12, 15, 13, 12, 14, 15, 14, 13, 14,
15, 14, 13, 16, 15, 13, 14, 15, 14, 15, 12, 16, 15, 17, 15, 14, 13,
14, 15, 13, 14, 16, 14, 15, 14, 15, 13, 15, 14, 15, 13, 15, 13, 15,
16, 13, 14, 15, 16, 14, 13, 15, 13, 16, 15, 13, 15, 16, 15, 14, 15,
13, 14, 15, 14, 13, 15, 14, 15, 14, 13, 14, 15, 14, 15, 16, 15, 14,
15, 14, 15, 14, 16, 14, 13, 14, 15, 14, 15, 14, 15, 14, 15, 14, 13,
14, 15, 14, 13, 14, 17, 14, 15, 14, 15, 13, 14, 13, 14, 16, 14, 15,
14, 13, 15, 13, 12, 13, 14, 15, 14, 15, 13, 14, 15, 14, 13, 14, 16,
14, 13, 14, 15, 16, 13, 14, 15, 13, 14, 13, 15, 14, 15, 16, 13, 14,
13, 14, 13, 14, 12, 15, 14, 15, 16, 14, 13, 15, 14, 15, 14, 15, 14,
13, 15, 13, 14, 13, 14, 15, 14, 15, 14, 15, 13, 14, 15, 13, 14, 16,
14, 15, 14, 13, 15, 14, 15, 14, 16, 15, 13, 16, 15, 13, 15, 14, 15,
16, 14, 15, 13, 14, 15, 14, 15, 12, 15, 13, 14, 16, 15, 13, 14, 15,
14, 15, 14, 15, 13, 14, 15, 14, 15, 14, 13, 15, 12, 14, 15, 13, 15,
12, 15, 14, 15, 14, 13, 15, 14, 15, 13, 14, 15, 14, 15, 12, 13, 15,
14, 15, 14, 13, 14, 15, 13, 16, 15, 14, 15, 14, 15, 13, 14, 15, 16,
15, 14, 15, 14, 15, 14, 15, 14, 16, 13, 15, 14, 16, 15, 14, 13, 14,
13, 14, 15, 14, 15, 14, 15, 14, 15, 13, 16, 13, 14, 13, 14, 15, 13,
15, 14, 16, 14, 15, 14, 15, 13, 15, 13, 14, 15, 14, 15, 14, 13, 14,
13, 14, 15, 13, 14, 15, 14, 15, 14, 15, 14, 15, 14, 15, 13, 15, 14,
15, 16, 14, 15, 14, 12, 14, 16, 14, 15, 14, 15, 14, 15, 13, 14, 13,
14, 12, 14, 13, 14, 15, 14, 15, 14, 15, 13, 15, 13, 16, 14, 15, 14,
15, 14, 15, 14, 15, 16, 14, 15, 13, 15, 13, 16, 14, 13, 14, 15, 13,
15, 13, 16, 15, 12, 14, 13, 16, 15, 14, 13, 14, 15, 17, 15, 14, 13,
14, 16, 15, 14, 13, 15, 14, 16, 15, 14 };
clock_t start, end;
float cpu_time_used;
start = clock();
// Do UKF
for (uint32_t i = 0; i < 500; i++) {
zk[0] = data[i];
X[i] = xhat[0];
ukf(xhat, zk, u, P, Q, R, a, k, b, L, ukf_transition);
}
end = clock();
cpu_time_used = ((float) (end - start)) / CLOCKS_PER_SEC;
printf("\nTotal speed was %f\n", cpu_time_used);
// Here is the filtered data
print(X, 500, 1);
return EXIT_SUCCESS;
}MATLAB code example.
function Unscented_Kalman_Filter()
% Initial parameters
L = 1;
a = 0.5;
b = 2;
k = 1;
Q = 0.0001;
R = 2;
P = 1;
xhat = 15;
zk = 13;
% Read the data - The log.txt file can be found at
% https://github.com/DanielMartensson/STM32-Libraries/tree/master/VL6180X/Distribution
fid = csvread('log.txt')';
l = 500;
% Filtered data
X = zeros(1, l);
for i = 1:l
% Get measurement
zk = fid(i);
% Save UKF value
X(i) = xhat;
% UKF filter
[xhat, P] = ukf(xhat, zk, P, Q, R, a, k, b, L);
end
close all
plot(1:l, X, 'r', 1:l, fid(1:l), 'b');
legend('UKF', 'Real')
grid on
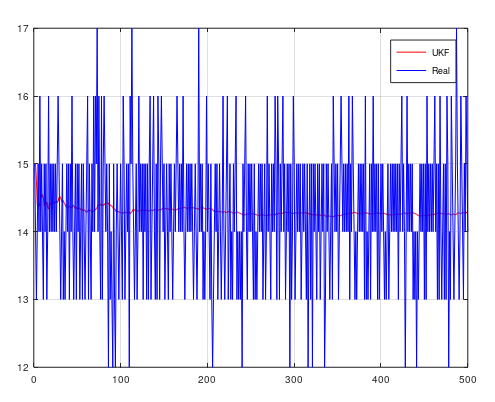
endHere I have measured with VL6180x laser from ST Microeletronics. It’s a very cheep laser and with UKF filter, this laser gives a very more accurate measurement. I have measure an object from a fixed distance.
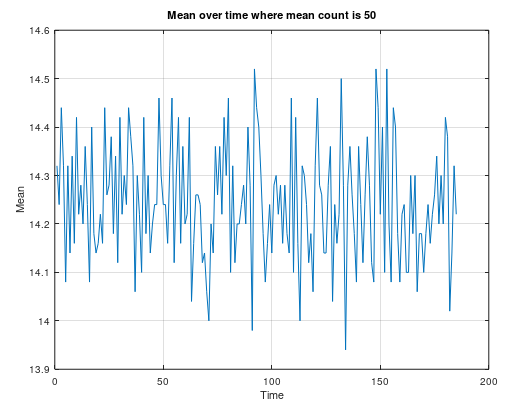
Here we can see at the average is about 14.5 mm if I made a moving average filter with 50 samples.
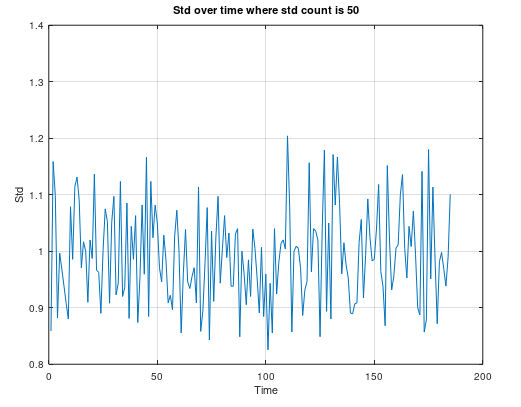
The deviation is about 1.5 mm.
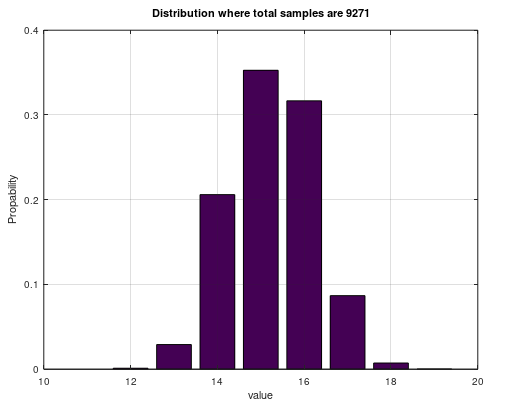
Total measurements give an average about 15 mm, but more closer to 14.5 mm.
Here you can see the results with the raw laser sensor distance measurement and UKF filter.