This package contains an ode based reservoir computer for learning time series data. The package also includes functions for generating and plotting time series data for three chaotic systems. It additionally contains a module that implements hyperparameter optimization for reservoir computers via the sherpa package.
The package is hosted on PyPi and can be installed with pip:
pip install rescomp
Alternatively, users can download the repository and add the location of the repo to their Python path.
Import the package with import rescomp as rc.
Currently, we support code to generate time series on three chaotic attractors. Time series can be generated with the orbit function and plotted in 3D with plot3d or in 2D with plot2d. (Plots are displayed in a random color so call the plot function again or supply color(s) to the keyword argument if it looks bad.)
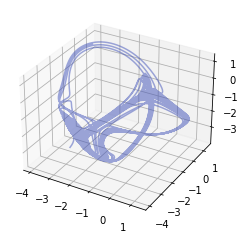
- Thomas' cyclically symmetric attractor
t, U = rc.orbit("thomas", duration=1000, dt=0.1)
fig = rc.plot3d(U)
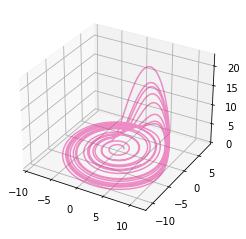
- The Rossler attractor
t, U = rc.orbit("rossler", duration=100, dt=0.01)
fig = rc.plot3d(U)
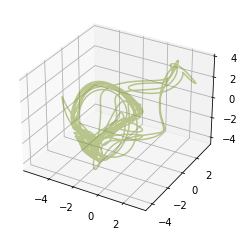
- The Lorenz attractor
t, U = rc.orbit("lorenz", duration=100, dt=0.01)
fig = rc.plot3d(U)
The package contains two options for reservoir computers: ResComp and DrivenResComp. The driven reservoir computers are still in beta stage but can be used for designing control algorithms [1]. Here is an example of learning and predicting Thomas' cyclically symetric attractor:
The train_test_orbit function returns training and testing sequences on the attractor. The test sequence immidiately follows the training sequence.
tr, Utr, ts, Uts = rc.train_test_orbit("thomas", duration=1000, dt=0.1)
Initialize the default reservoir computer and train on the test data with:
rcomp_default = rc.ResComp()
rcomp_default.train(tr, Utr)
Take the final state of the reservoir nodes and allow it to continue to evolve to predict what happens next.
r0 = rcomp_default.r0
pre = rcomp_default.predict(ts, r0=r0)
fig = rc.plot3d(pre)
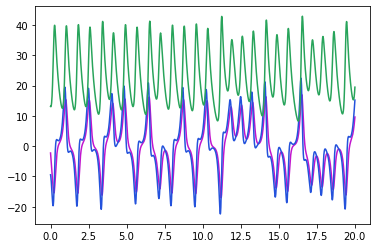
This doesn't look much like Thomas' attractor, suggesting that these parameters are not optimal.
Optimized hyper parameters for each system are included in the package. Initialize a reservoir with optimized hyper parameters as follows:
hyper_parameters = rc.SYSTEMS["thomas"]["rcomp_params"]
rcomp = rc.ResComp(**hyper_parameters)
Train and predict as before.
rcomp.train(tr, Utr)
r0 = rcomp.r0
pre = rcomp.predict(ts, r0=r0)
fig = rc.plot3d(pre)
This prediction looks much more like Thomas' attractor.
The rescomp.optimizer package contains a class, ResCompOptimizer, that allows for easily performing hyperparameter optimization on a ResComp or DrivenResComp object:
from rescomp.optimizer import ResCompOptimizer
rcopt = ResCompOptimizer('thomas', 'relax', 'random', 'augmented')
rcopt.run_optimization(50, 20)
optimized_hyperparams = rcopt.get_best_result()
Also of note are the methods generate_orbits() and run_tests().
generate_orbits() will generate a given number of orbits from the system as well as the reservoir computer's prediction, which is useful for visual comparisons.
run_tests() will test the reservoir computer on continued and random predictions with the given hyperparameters, as well as calculate the derivative fit of its predictions and estimate the Lyapunov exponent of the reservoir dynamical system.
There are four built-in systems: the Lorenz, Thomas, and Rossler chaotic attractors, as described above; and a set of data from a soft robot dynamical system.
Other systems can be created by extending the rescomp.optimizer.System class, and can be passed to the optimizer instead of the system string.
There is also a script module, rescomp.opt_then_test, that will run hyperparameter optimization on a ResComp on a given system, run various tests on the optimized hyperparameters, and save the results.
The script can be run as follows:
python3 -m rescomp.opt_then_test [args]
For details on what parameters it accepts, run it as:
python3 -m rescomp.opt_then_test -h
[1] Griffith, A., Pomerance, A., Gauthier, D.. Forecasting Chaotic Systems with Very Low Connectivity Reservoir Computers (2019)