Controller 101 + Transforms 101 (#224)

* Controller 101

* Add next steps

* Moved Controller 101 to Service Overviews

* Going overboard on transforms / poses explanation

* Splitting and reorganization

* Change Controller 101 name + minor changes

---------

Co-authored-by: Kyle Coble <kwc57@cornell.edu>

circuitpy/lib/farm_ng/utils/main_loop.py

@@ -47,7 +47,7 @@ def get_node_id():
     except OSError:
         node_id = 0x42
 
-    print(f"node_id = 0x{node_id:0x}")
+    print(f"node_id = 0x{node_id: 0x}")
     return node_id
 
 
@@ -114,7 +114,7 @@ def io_debug_str(self):
 
         if self.show_time:
             ticks_now_ms = ticks_ms()
-            debug.write(f"up:{monotonic()-self.t0:.1f}\n")
+            debug.write(f"up: {monotonic() - self.t0: .1f}\n")
         if self.show_can_dts:
             for key, value in sorted(DtTracker._g_trackers.items()):
                 debug.write(f"{key: <20}: {int(value.mean_dt()): <5d} age: {value.age(ticks_now_ms)} \n")
@@ -151,7 +151,7 @@ def handle_message(self, message):
         if self.show_can_dts:
             dt = self.can_id_dts.get(message.id)
             if dt is None:
-                dt = DtTracker(f"can/0x{message.id:03x}")
+                dt = DtTracker(f"can/0x{message.id: 03x}")
                 self.can_id_dts[message.id] = dt
             dt.update()
 
@@ -236,7 +236,7 @@ def draw_debug(self, display: Display):
 
         if self.show_time:
             ticks_now_ms = ticks_ms()
-            debug.write(f"up:{monotonic()-self.t0:.1f}\n")
+            debug.write(f"up: {monotonic() - self.t0: .1f}\n")
             for key, value in DtTracker._g_trackers.items():
                 if key.startswith("can/"):
                     continue

website/docs/concepts/controller_101/README.md

@@ -0,0 +1,93 @@
+---
+id: create-and-propagate-poses
+title: Create and Propagate Poses
+---
+
+## Understanding Transforms and Poses
+
+Before we can send our robot out to drive a **track** (or **path**),
+we need to understand where our robot is and where we want to send it.
+For that purposes, please refer to **[Concepts - Transforms and Poses](/docs/concepts/transforms_and_poses)**
+before continuing on with this overview.
+
+## Creating and Propagating Poses for the Controller
+
+When you want the Amiga to perform a specific movement, you need to provide it with a series
+of poses that describe that movement.
+We call these poses **waypoints** and the series of them a **track*.*
+
+For a better understanding of the `Pose` structure, please refer to our
+[`Pose` proto overview](/docs/concepts/transforms_and_poses/#the-farm-ng-pose-proto).
+
+### Example
+
+There are several ways of creating poses and commanding your `Controller` to follow them.
+Let's check how to use the concepts learned here to create poses that represent a `pi turn`
+(also know as a U turn) using the `pose` structure:
+
+**NOTE**: Please note that in this example we propagate the proposes from the robot frame.
+
+```python
+def create_pi_turn_segment(
+    previous_pose: Pose3F64, next_frame_b: str, radius: float, spacing: float = 0.1
+) -> list[Pose3F64]:
+    """Compute a pi turn segment.
+
+    Args:
+        previous_pose (Pose3F64): The previous pose.
+        next_frame_b (str): The name of the child frame of the next pose.
+        radius (float): The radius of the pi turn.
+        spacing (float): The spacing between waypoints, in meters.
+
+    Returns:
+        list[Pose3F64]: The poses of the pi turn segment.
+    """
+    # Calculate the total arc length of the half-circle
+    arc_length = pi * radius
+
+    # Determine the number of segments, ensuring at least one segment
+    num_segments = max(int(arc_length / spacing), 1)
+
+    # Angle increment per segment
+    delta_angle = pi / num_segments
+
+    # Distance increment per segment
+    delta_distance = arc_length / num_segments
+
+    # Create a container to store the track segment waypoints
+    segment_poses: list[Pose3F64] = [previous_pose]
+
+    for i in range(1, num_segments + 1):
+
+        # Calculate the pose for the current segment
+        turn_segment: Pose3F64 = Pose3F64(
+            a_from_b=Isometry3F64([delta_distance, 0, 0], Rotation3F64.Rz(delta_angle)),
+            frame_a=segment_poses[-1].frame_b,
+            frame_b=f"{next_frame_b}_{i-1}",
+        )
+        segment_poses.append(segment_poses[-1] * turn_segment)
+
+    # Rename the last pose to the desired name
+    segment_poses[-1].frame_b = next_frame_b
+    return segment_poses
+```
+
+### Code Breakdown
+
+Since we're in the robot frame, we always command it to drive forward, for this reason the `y` and `z`
+components of our `Isometry3F64` are always zero.
+
+- The robot moves forward by delta_distance (linear movement along the x-axis).
+- It rotates by delta_angle about the z-axis.
+- This transformation is then used to calculate the new pose of the robot for that segment.
+
+In essence, by using Isometry3F64, you're able to succinctly describe both the linear and
+angular movements of the robot for each segment of its pi turn.
+
+## Next Steps
+
+Make sure to check the [Concepts](https://amiga.farm-ng.com/docs/concepts/) page
+to know more about all the services available in your Amiga and how they interact with each other.
+
+Make sure to also check our [Brain Controller Examples](https://amiga.farm-ng.com/docs/examples/examples-index)
+to test the `Controller` in your Amiga.

website/docs/concepts/transforms_and_poses/README.md

@@ -0,0 +1,159 @@
+---
+id: transforms-and-poses
+title: Transforms and Poses
+---
+
+## Fundamental Concepts
+
+Before we can create autonomy applications for our robot,
+we need to understand where our robot and other points of reference are.
+The following concepts are critical to understand if you wish
+to develop autonomous robotics applications with your Amiga.
+
+### Frames of Reference
+
+In robotics, a **frame of reference**
+(often called a "**frame**", **coordinate frame**, or "**reference frame**")
+is a description of a coordinate system of 3 orthogonal axes (**x**, **y**, & **z**) defined by
+the position and orientation of the object.
+
+The two primary frames you need to be aware of are:
+
+**World Frame (`world`)**:
+Conventionally, this is a fixed frame representing the environment in which the robot operates.
+Think of it as an anchor point that doesn't move.
+If using RTK GPS, a typical world frame coordinate system is defined at the location
+of your RTK base station.
+
+**Robot Frame (`robot`)**: This frame is attached to the robot.
+As the robot moves, this frame moves with it.
+Considering the robot is not a single point, it is important to define where on the robot
+is considered the center of the `robot` frame axes.
+At farm-ng we choose the center of the robot (in length & width) at ground level.
+
+Additional relevant frames for your Amiga-based robotics applications
+may include the `camera` frame, the `imu` frame, the `gps_antenna` frame, and so on.
+
+Each **reference frame** is represented below as a set of red-green-blue axes.
+The frames are connected by 6 degree-of-freedom **transforms**,
+represented below by yellow arrows.
+
+<!-- ![reference](https://foxglove.dev/images/blog/understanding-ros-transforms/hero.webp) -->
+![image](https://github.com/farm-ng/amiga-dev-kit/assets/53625197/656fff08-0296-4d81-8990-dc65d7f1af16)
+
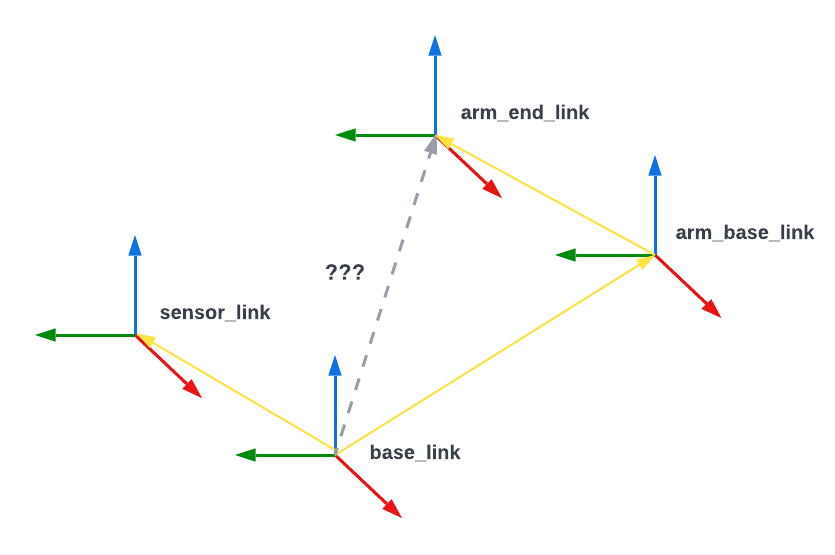+*Image Credit: [https://foxglove.dev/blog/understanding-ros-transforms](https://foxglove.dev/blog/understanding-ros-transforms)*
+
+### Transformations
+
+A **transformation**, or **transform**, describes how to move from one reference frame to another.
+
+Typically in robotics we represent these transforms as an **isometry** transformation in 3D space.
+This is a distance-preserving 6 degree-of-freedom (DOF) transformation
+that includes a translation (3 DOF) and a rotation (the other 3 DOF).
+
+For instance, we can represent the transformation from the `world` reference frame
+to the `robot` reference frame.
+Our naming convention at farm-ng is to call this the **`world_from_robot`** transformation,
+following a `<parent>_from_<child>` or `<frame_a>_from_<frame_b>` naming convention.
+
+This transform contains the **translation** along the `world` **x, y, z** axes,
+as well as the **rotation** required to align the axes.
+
+The **translation**, a 3-dimensional linear offset,
+is represented as a vector of `[x, y, z]` coordinates in the parent reference frame.
+
+The **rotation**, a 3-dimensional rotation, can be represented in a number of ways,
+but typically is represented as a **quaternion**.
+
+#### Quaternions
+
+Quaternions are a type of mathematical object used to represent rotations in 3D space.
+
+Quaternions consist of four numbers `(x, y, z, w)` (or sometimes in order `(w, x, y, z)`).
+`w` represents the scalar (or real) part of the rotation
+and `x`, `y`, and `z` are the vector (or imaginary) parts.
+
+Quaternions are an alternative to other methods like Euler angles or rotation matrices.
+Quaternions are particularly useful because they are compact,
+avoid certain problems like gimbal lock, and can be more computationally efficient.
+
+#### Transform math
+
+**Transforms** can be mathematically manipulated to understand where **coordinate frames**
+are in relation to one another.
+Most commonly, you will **invert** transforms and you will **multiply** transforms.
+
+If you know the transform from the `world` coordinate frame to the `robot` coordinate frame (`world_from_robot`),
+you can **invert** that transform to get the transform from the `robot` coordinate frame
+to the `world` coordinate frame (`robot_from_world`).
+
+```python
+world_from_robot = robot_from_imu^-1
+```
+
+If you know two transforms with a common frame, you can **multiply** them.
+
+Say you know `world_from_robot` and the `robot_from_imu` transform from your
+`robot` frame to your `imu` frame (where the IMU is on your robot).
+You can calculate the transform from the `world` frame to the `imu` frame (`world_from_imu`)
+with transform **multiplication**.
+
+```python
+world_from_imu = world_from_robot * robot_from_imu
+```
+
+### Poses
+
+We tend to think of where our robot is as a **pose**, a combination of **position** and **orientation**.
+The **position** being where the robot is, and the **orientation** being which way the robot is facing.
+
+A pose is, however, undetermined as there needs to be a **frame of reference** the position
+and orientation are in.
+Queue **transforms**!
+
+We can define the **pose** of our robot as the 6-DOF transformation from the `world` frame
+to our `robot` frame (`world_from_robot`).
+
+We are not limited to representing the `world_from_robot` transformation as a pose.
+Any transform can be represented as a pose by correctly specifying the `frame_a` (parent frame)
+and `frame_b` (child frame) in our
+[**`Pose` protobuf definition**](https://github.com/farm-ng/farm-ng-core/blob/main/protos/farm_ng/core/pose.proto).
+
+### The farm-ng `Pose` proto
+
+:::info
+For the latest definition of the `Pose` structure, please refer to our
+[**`Pose` protobuf definition**](https://github.com/farm-ng/farm-ng-core/blob/main/protos/farm_ng/core/pose.proto).
+:::
+
+Each pose has an `Isometry3F64`, which is a representation of rigid body transformations in 3D space.
+In simple terms, it describes how an object moves and rotates in three-dimensional space
+without changing its shape.
+The term "isometry" implies that distances between points remain unchanged during the transformation.
+
+In the context of robotics, `Isometry3F64` is used to describe the movement
+and rotation of a robot in 3D space.
+
+#### Properties of Isometry3F64
+
+**Translation**: This represents the linear movement of the robot.
+This is represented as a 3D vector, where each component (x, y, z) describes movement along that axis.
+
+**Rotation**: This represents the angular movement of the robot.
+This rotation is represented using `Rotation3F64`, which, in this context, uses the Rz method
+to denote a rotation about the z-axis.
+
+**Rz method**: The Rz method, when applied to Rotation3F64, denotes a rotation about the z-axis.
+In 3D space, the z-axis typically points upwards, perpendicular to the ground plane
+(assuming the x-y plane represents the ground).
+When you rotate an object about the z-axis, it turns around this vertical line,
+much like how a spinning top rotates around its central axis.
+
+### Resources
+
+The use and multiplication of coordinate frame transforms is a fundamental concept in robotics!
+As such, there is an abundance of quality, free resources on the topic.
+
+For a slightly-less-brief introduction you can refer to [Understanding ROS Transforms](https://foxglove.dev/blog/understanding-ros-transforms).
+
+If you wish to dive deeper on this topic, one option is [MIT OpenCourseWare - Introduction To Robotics](https://ocw.mit.edu/courses/2-12-introduction-to-robotics-fall-2005/).

website/sidebars.js

@@ -112,10 +112,14 @@ const sidebars = {
       "support/github-101",
     ],
   },
-  "Conepts": [
+  "Concepts": [
     "concepts/concepts-index",
     {
-      "Service Overviews": [
+      "Fundamental Concepts": [
+        "concepts/transforms_and_poses/transforms-and-poses",
+        "concepts/controller_101/create-and-propagate-poses",
+      ],
+        "Service Overviews": [
         "concepts/canbus_service/canbus-overview",
         "concepts/oak_service/oak-overview",
         "concepts/gps_service/gps-overview",