Lem In 🐜

🇺🇸 Subject

🇫🇷 Subject

💦 Lem In is an algorithmic project about a maximum flow problem in graph theory.

The goal is to find the optimal flow of ants through an anthill while minimizing the number of rounds to cross it.

Check that video (from another student) to visualize what it is all about 💁🏼‍♀️

Ant farm description:

Rooms are defined by: name coord_x coord_y

Links are defined by: name1-name2

All of it is broken by comments, which start with #

Graphical representation:

The program receives the data describing the ant farm from the standard output in the following format:

• number of ants
• Ant farm description

There is always a "start" room and an "end" room. These rooms are preceded by a #start or #end comment.

At the beginning, all ants are inside the "start room". The goal is to bring them to the "end room".

Solution: improved Breadth-First Search (BFS)

The solution can be one or multiple paths. If you have only one ant, you'll need only one path but if there is more than one ant, you might consider finding more paths 🔎

To find the best (and good number of) paths, I used an algorithm inspired by Breadth-first search

👩🏼‍💻 Bradth-first search

🚨 Bradth-first search is not optimal

However, this solution is flawed because it may prevent the program to find multiple paths.

For example, this solution is not optimal because a BFS find only one path when the most efficient solution would be to find two paths.

✅ Modified Bradth-first search

When looking for more than one path, we decided to modify the BFS algorith and allow using an occupied room to find more path.

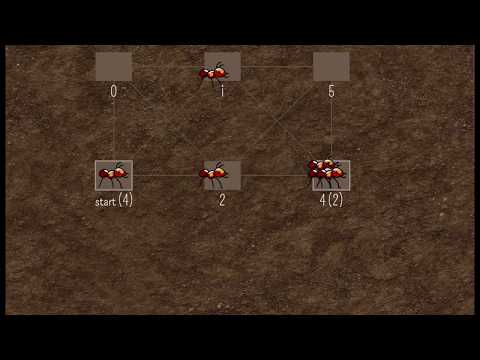
Here is an example:

• Step 1: find the shortest path

• Step 2: find more paths

The goal here is to find as much path as we can without using an occupied room.

• Step 3: find more path WITH occupied room

The goal here is to see if we can replace a path by two (or more) paths. To do so, we are now allowed to use an occupied room. If we do, we will have to go back one time minimum.

Done 🎉

Result

The result has the following format:

number of ants
ant farm description
Lx-y Lz-w Lr-o ...

x, z, r are ant number

y, w, o are room names.

Test it!

clone the project

make

./lem-in < map

You can also create your own map 💁🏼‍♀️

Credits

This project was made by @tlamart and @mpicard