This project was undertaken as part of the Independent Inquiry course at Sacred Heart Preparatory. To my knowledge, it was the first science research done in this course. I had very little access to university level mentorship and resources, and I was unable to work with anyone in the field of computational biology. Despite the various difficulties, I was able to independently learn the basics of working with right-censored data and familiarize myself with various survival analysis techniques.
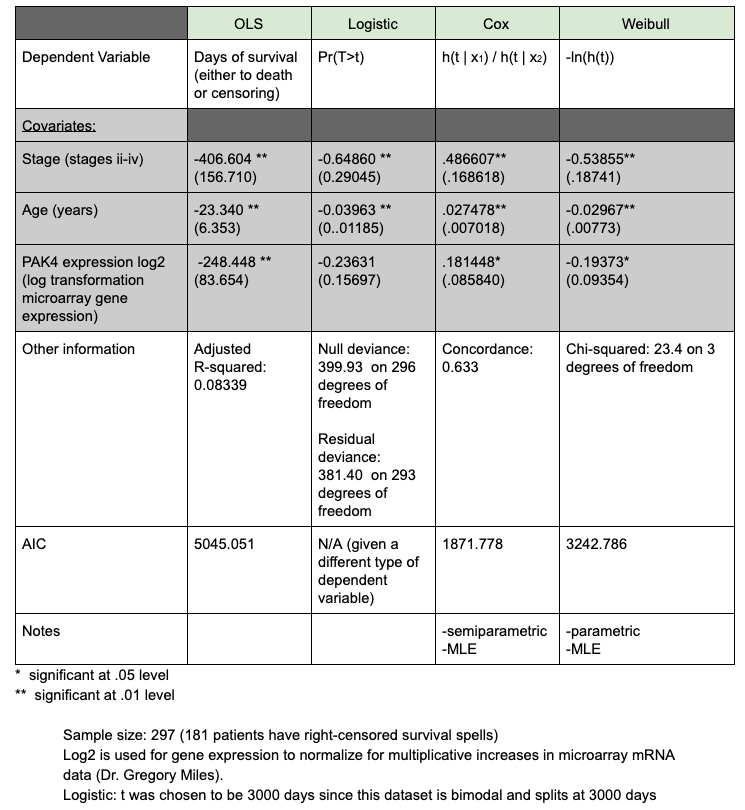
The goal of my project changed over the course of the year as I learned more about what was feasible in the relatively short time frame and for the limited resources available. By the end of the year, I decided to tie my work together by summarizing my findings about 4 different statistical estimators (OLS, logistic regression, the Cox proportional hazards model, and the Weibull proportional hazards model). I compared these using AIC in an effort to understand which is best suited to mortality data (results in the least information loss).
All the data in my research was obtained from the National Institute of Health’s The Cancer Genome Atlas (NIH TCGA). Because I was not associated with a lab, my access to data was limited (e.g., I did not have access to whole-genome sequencing data or miRNA sequencing data), but I was nevertheless able to pull enough data to run my “proof-of-concept” comparison.
In order to import the data from the NIH TCGA, I used FirebrowseR, a package on GitHub designed by Mario Deng to use the Broad Institute’s Firebrowse Web API.
After removing outliers from my dataset, it consisted of 297 patients with 128 variables.
It is clear from the very low R-squared that this is an inadequate model for this data. This is for a couple of reasons. First, OLS is a parametric model, meaning it assumes an underlying distribution, which may or may not apply to the data. While certain adjustments can be made to the covariates to compensate for this, it somewhat limits the kinds of data the model applies to. Second, and more importantly, OLS does not account for censored data. For my data, I used a somewhat arbitrary duration for my dependent variable (See Appendix 1), and as a result, the data points cut off at a particular threshold (since this data was collected around the same time).
Considering the logistic model, it does somewhat account for censored data (since we can say with certainty they lived over a certain number of days); however, the output provides limited information. In order to fit this data, the continuous dependent variable had to be reduced to a binary one, resulting in a loss of information. Another difficulty is that the logistic model requires choosing a threshold time t. This data happened to be bimodal, meaning there was a natural cutoff point at 4000 days, but this may not hold true for all samples.
Both the Weibull and Cox performed significantly better than OLS, with lower AIC scores. Cox and Weibull account for censored data since they calculate a hazard ratio, which is based on the probability of death. Censored observations are simply not considered in this probability after they are censored. The main difference between the two models is that Weibull is parametric, while Cox is nonparametric, allowing it to better fit the data. This is likely why Cox outperformed Weibull in this instance. However, if the shape of the Weibull model was known, the Weibull model would generally outperform the Cox model.
Models which account for censored data are more suitable for cancer datasets, which usually include patients who are alive, as well as those who are dead. In the future, Cox and Weibull could both be used to determine the statistical significance of genetic and environmental factors in the severity of cancer. Such observations could lead to new discoveries about the ways in which tumors grow and become malignant.